XXIII Convegno UMI-CIIM (Loano, Italy, 3-5 october 2002): author’s lecture

STORIA DELLE SCIENZE PER LA DIDATTICA

“Controversie” tra il XVII e il XVIII secolo

Giorgio T. Bagni

Dipartimento di Matematica,

Università di Roma “La Sapienza”

Abstract The History of Sciences is a very important tool for Didactics. In this paper we propose two historical examples: a mathematical one, based upon the debate about the logarithms of negative numbers (xviii century); and a physical one regarding the introduction of the concepts of work and of kinetic energy based upon a geometric analogy according to Gian Maria Ciassi’s work (1654-1679). An important educational problem consists in the verify of the learning; so we expose an experimental research related to the mathematical example presented.

1. “ESISTONO” I LOGARITMI DEI NUMERI NEGATIVI?

La storia delle scienze è un prezioso elemento per una corretta didattica, tale da favorire, negli allievi, un accostamento efficace ai concetti ed ai procedimenti ed un apprendimento cosciente e profondo, una vera, ampia formazione culturale (Pizzamiglio, 2002)[1]. Nel presente lavoro ci occuperemo di due esempi, tratti dalla storia della matematica e della fisica, che potranno essere utilmente riferiti alla didattica della scuola secondaria superiore[2].

La questione della natura dei logaritmi dei numeri negativi fu sollevata da una lettera di Leibniz a Giovanni Bernoulli del 16 marzo 1712 (Giusti, 1982; per il testo originale si veda: Leibniz, 1856); a tale riguardo, gli studiosi del tempo erano divisi in due schieramenti: molti sostenevano l’opinione di Leibniz, poi ripresa da Euler (Euler, 1749; Langer, 1935), Walmesley (Walmesley, 1748) e in Italia, tra gli altri, da Fontana (Fontana, 1783 e 1799) e da Franceschinis (Franceschinis, 1787), secondo la quale i logaritmi dei numeri negativi avrebbero dovuto essere interpretati come quantità immaginarie (Naux, 1971; Bagni, 1991a e 1994).

Contrario a quest’opinione era un gruppo di matematici guidato da Giovanni Bernoulli (Caldani, 1782 e 1791, Ferroni, 1782, Frisi, 1782 e d’Alembert; si veda: Franceschinis, 1787), il quale proponeva di considerare reali tali logaritmi e di porre (Loria, 1929-1933) log(-x) = logx in base all’osservazione:

2log(-1) = log(-1)² = log(+1)² = 2log(+1)

Anticipiamo che, dal punto di vista moderno, sarà Leonhard Euler nel 1747 a chiarire la questione[3] applicando la celebre formula: e^iz = cosz+i×sinz. Ponendo, in essa, z = pi, infatti, si ottiene e^i(pi) = -1 da cui log_e(-1) = i(pi). Euler proverà anche che ciascun numero ammette, in ambito complesso, infiniti logaritmi; infatti dalla formula e^iz = cosz+i×sinz, con k appartenente a Z segue che:

log_ea = b implica che log_ea = b+2k(pi)×i

Osserviamo che la posizione bernoulliana secondo la quale risulta log(-x) = logx porta ad una considerazione della curva logaritmica costituita da due rami simmetrici rispetto all’asse delle ordinate; ciò è indicato da molti sostenitori della realtà dei logaritmi dei numeri negativi, tra i quali Vincenzo e Giordano Riccati (Riccati, 1778a e 1778b; Riccati, 1789). Giordano Riccati afferma:

«La vera equazione della Logistica […] ha due rami affatto simili, e dall’assintoto equidistanti, onde ci sono forniti i logaritmi di’ numeri negativi eguali a quelli de’ numeri postivi» (Riccati, 1778a).

Un brillante allievo di Vincenzo Riccati nello studio bolognese è il trentino Giovanni Francesco Giuseppe Malfatti (1731-1807): anch’egli contestò, seppur velatamente, la posizione riccatiana sulla realtà dei logaritmi dei numeri negativi (Malfatti, 1795). Malfatti assunse però una posizione di mediazione, forse (Giusti, 1982) per confermare il rispetto e la gratitudine nei confronti del proprio maestro; in sostanza, Malfatti sottolinea che la curva logaritmica di equazione y = logx non può essere considerata coincidente con la curva di equazione 2y = logx² essendo questa seconda equazione esprimibile da y = log[abs(x)] (dove abs(x) indica il valore assoluto di x). I due rami della curva logaritmica risultano quindi propri soltanto del grafico di y = log[abs(x)], non di y = logx (dal punto di vista didattico, una simile questione è studiata ad esempio in: Bagni, 2000).

2. UN’ESPERIENZA DIDATTICA

Le considerazioni storiche esposte sono state applicate in una ricerca didattica sperimentale in cui sono state coinvolte due classi di IV e due classi di V liceo scientifico (per un totale di 92 allievi; le prove sono state effettuate a Treviso nel 1999). Gli allievi di tali classi conoscevano i logaritmi, la funzione valore assoluto, i numeri complessi (ma non avevano trattato la “formula di Eulero”).

È stata inizialmente fornita a ciascun allievo la scheda seguente:

Scheda A

In un libro del Settecento che si occupa di logaritmi si legge:

Sappiamo che: log₂64 = 6 allora: log₂8² = 6

e anche: log₂(-8)² = 6 ma allora è: 2log₂(-8) = 6

Dunque concludiamo: log₂(-8) = 3

Sei d’accordo con l’autore del libro? Giustifica la tua risposta.

Si osservi che, in questa fase, abbiamo ritenuto non opportuno segnalare esplicitamente la conseguenza log₂(-8) = 3 Þ 2³ = -8 che si otterrebbe applicando la definizione di logaritmo per evitare di forzare alcune risposte.

Riportiamo i risultati nella seguente tabella:

Scheda A (92 allievi: 48 di IV liceo scientifico, 44 di V liceo scientifico)
	IV liceo	V liceo	Totale
D’accordo con l’autore del libro	13	7	20 (22%)
Non d’accordo con l’autore del libro	27	26	53 (57%)
Altre risp. o nessuna risp.	8	11	19 (21%)

Notiamo che la differenza di comportamento tra gli allievi delle IV e delle V classi non appare rilevante (la stessa osservazione potrà essere ripetuta per le risposte nelle schede che saranno presentate nel seguito di questo paragrafo).

Per quanto riguarda le giustificazioni degli allievi, alcune affermazioni sono interessanti; tra chi ha rifiutato l’affermazione riportata nella scheda A troviamo:

“Il dominio è costituito dai soli reali positivi” (Isabella, classe IV).

“La proprietà si applica solo se tutti i logaritmi coinvolti esistono reali, altrimenti non si può lavorare su cose che non ci sono” (Maurizio, classe V).

Un allievo osserva che l’esempio proposto coinvolge un quadrato, 8², (e finirà quindi per negarne una validità generale):

“64 è un quadrato perfetto, cioè un caso particolare” (Aldo, classe IV).

Alcuni allievi, pur rifiutando infine il procedimento indicato, ritengono di dover comunque esprimere qualche perplessità:

“Il procedimento sembrerebbe giusto ma contrasta con le condizioni da porre” (Carlo, classe V).

Altri invece accettano il procedimento osservando semplicemente che:

“L’autore del libro ha applicato la proprietà” (Giuseppe, classe IV).

Allo stesso gruppo di allievi abbiamo quindi proposto la seguente scheda:

Scheda B

Nel 1795, il matematico Giovanni Francesco Giuseppe Malfatti (1731-1807) ha osservato che:

la curva logaritmica di equazione y = logx

non può essere considerata coincidente con la curva di equazione: 2y = logx²

in quanto questa seconda equazione può essere scritta nella forma: y = log[abs(x)]

Sei d’accordo con Malfatti?

Riportiamo i risultati nella seguente tabella:

Scheda B (92 allievi: 48 di IV liceo scientifico, 44 di V liceo scientifico)
	IV liceo	V liceo	Totale
D’accordo con Malfatti	43	39	82 (89%)
Non d’accordo con Malfatti	4	2	6 (7%)
Altre risp. o nessuna risp.	1	3	4 (4%)

Abbiamo infine chiesto agli allievi di riconsiderare la risposta data al quesito della scheda A, con la possibilità di confermare o di cambiare liberamente la risposta precedentemente data[4]. Riportiamo i risultati nella seguente tabella:

Scheda A (seconda considerazione) (92 allievi: 48 di IV liceo scientifico, 44 di V liceo scientifico)
	IV liceo	V liceo	Totale
D’accordo con l’autore del libro	3	2	5 (5%)
Non d’accordo con l’autore del libro	37	39	76 (83%)
Altre risp. o nessuna risp.	8	3	11 (12%)

Dunque un non trascurabile numero di allievi orienta diversamente la propria opinione: se prima della considerazione della nota di Malfatti il 57% degli allievi dichiarava di optare per la risposta corretta, dopo l’esame della posizione malfattiana (accettata dall’89% degli allievi) tale percentuale è salita all’83%.

Scopo del presente lavoro è comunque soltanto quello di segnalare la possibilità di introdurre un esempio storico che possa stimolare ed orientare utilmente gli allievi: sulla questione, infatti, molti altri test potrebbero essere ideati e somministrati agli studenti. Inoltre osserviamo che una ricerca didattica completa dovrebbe essere corredata da una più profonda e dettagliata analisi delle caratteristiche originali dell’insegnamento degli argomenti trattati (ad esempio della nozione di logaritmo) e da interviste sistematiche: prima di trarre conclusioni definitive si dovrebbe ad esempio chiarire quale sia stata l’effettiva comprensione da parte degli allievi del collegamento tra l’osservazione di Malfatti e l’esempio proposto nella prima scheda.

Possiamo tuttavia concludere che la proposizione di un esempio storico appare utile per porre in termini corretti un problema didatticamente rilevante e, in alcune situazioni, anche per impostare il suo superamento.

3. UNA CELEBRE CONTROVERSIA FISICA: LA QUESTIONE DELLE “FORZE VIVE”

Concluderemo il presente lavoro con l’indicazione di un ulteriore esempio storico collegato alla didattica della matematica e della fisica (ci riferiamo a: Michieli, 1944; Bagni, 1991b e 2002) che può apparire interessante ad esempio con riferimento ai curricula della secondaria superiore.

Storicamente, il problema intorno al quale si sviluppò il dibattito sulle “forze vive” fu la determinazione della grandezza fisica da considerare causa del moto di un corpo: secondo Cartesio (René Descartes, 1596-1650) ed i pensatori di ispirazione cartesiana (Michieli, 1949a), un oggetto in movimento compirebbe lavoro a spese della propria quantità di moto (“quantitas motus”), ovvero del prodotto della propria massa per la velocità del moto stesso. Per contrastare tale affermazione che, com’è oggi noto, si rivelerà errata, Gottfried Wilhelm Leibniz (1646-1716) pubblicò la memoria dal titolo Brevis demonstratio erroris memorabilis Cartesii, et aliorum circa legem naturalem, secundum quam volunt a Deo eamdem semper quantitatem motus conservari; qua et in re mechanica abutuntur[5]. Al grande pensatore di Lipsia è sufficiente descrivere un semplice esperimento per concludere che la quantità di moto non può essere considerata la grandezza fisica a spese della quale un corpo si muove (e quindi, modernamente, compie lavoro): risultava dunque necessario definire in termini radicalmente nuovi una “forza motrice”.

La “vis motrix”, che sarà introdotta dallo stesso Leibniz nella memoria Specimen dynamicum pro admirandis naturae legibus circa corporum vires et mutuas actiones detergendis et ad suas causas revocandis del 1695, sostituì quindi nella storia della fisica la cartesiana quantità di moto nel ruolo di “serbatoio energetico” a spese del quale un corpo compie lavoro: ma questa “vis motrix”, o “vis viva”, non venne definita con precisione neppure da Leibniz, il quale si limitò a distinguerla dalla “forza morta”, intesa come una semplice pressione; si trattava, comunque, di una grandezza fisica nuova, proporzionale non alla velocità del corpo considerato (come accadeva per la quantità di moto), ma al quadrato di tale velocità[6].

Con la sensibilità del nostro tempo, rileviamo che anche l’impostazione leibniziana era concettualmente carente: l’imprecisione di Leibniz consisteva nel continuare a collegare, più o meno esplicitamente, la grandezza introdotta al concetto di forza. La “forza viva” di Leibniz non può essere considerata una vera e propria forza: l’approssimazione con cui sembra essere affrontata, tra il xvii ed il xviii secolo, l’intera questione è causata dalla mancanza di una precisa consapevolezza del concetto di lavoro (quindi di energia). L’introduzione della forza viva da parte di Leibniz deve comunque essere considerata una svolta per la storia della fisica: l’energia associata ad un corpo in movimento (energia cinetica) è infatti proporzionale al quadrato della velocità raggiunta dal corpo in esame, proprio come accade per la “vis motrix” leibniziana. Perciò a Leibniz viene attribuito un ruolo primario nella soluzione del problema delle forze vive.

4. LA POSIZIONE DI UN GIOVANE BOTANICO

Nella disputa sulle forze vive si inserisce la figura del botanico e fisico Gian Maria Ciassi (1654-1679)[7], autore del Tractatus physicomathematicus pubblicato insieme alle Meditationes de natura plantarum a Venezia nel 1677; in questo lavoro alcune osservazioni lasciano trasparire l’intuizione della soluzione del problema delle forze vive (Nicolai, 1754; Pellizzari, 1830, Rambaldi, 1863; un’edizione critica del Tractatus è in: Bagni, 1991b).

Le ricordate opere (gli unici lavori pubblicati da Ciassi nella sua breve vita: Ciassi, 1677) sono contenute nel piccolo volume dedicato al patrizio veneziano Gerolamo Correr (108 ff. in-12, corredato da undici tavole incise) così intestato:

Meditationes de natura plantarum,

et Tractatus physicomathematicus

De Æquilibrio praesertim fluidorum,

ac de levitate ignis.

Auctore

Ioanne Maria Ciasso

P. M. D.

Venetiis m.dc.lxxvii.

Apud Benedictum Milochum.

Superiorum Permissu.

Dalla lettura dell’opera si evince che Ciassi opera nel campo della meccanica attraverso l’uso elementare ma corretto dello strumento matematico: quasi tutte le sue dimostrazioni sono basate su semplici considerazioni geometriche (soprattutto sulla similitudine di figure e sulla proporzionalità di grandezze).

Il Tractatus si apre con alcune considerazioni di idrostatica applicate alla botanica, in cui l’Autore riprende la questione, già trattata nelle Meditationes de natura plantarum, della salita del liquido dalle radici alle altre parti della pianta; l’ipotesi secondo la quale tale fenomeno sarebbe collegato alla pressione esercitata dall’atmosfera sui liquidi stessi porta Ciassi a riferirsi al principio dei vasi comunicanti. Lo scienziato si propone quindi di precisare meccanicamente il fenomeno ipotizzato, ovvero di spiegare come le parti sovrastanti di un fluido agiscono su quelle sottostanti; a tale scopo, egli presenta un dettagliato approfondimento della meccanica delle leve, collegando alcune considerazioni geometriche al problema dell’equilibrio dei fluidi: Ciassi paragona la situazione statica di una leva a bracci diseguali a quella che caratterizza l’equilibrio di un fluido in vasi comunicanti diversi. Questa è la parte più interessante dell’intero lavoro ciassiano, riferita alla figura che riportiamo (tratta da: Ciassi, 1677, p. 54). Ciassi dimostra geometricamente attraverso la similitudine dei triangoli CAE e CDB la proporzione: AC : CD = AE : BD e da questa, essendo: GK = HE = AE/2 e FL = ID = BD/2, giunge infine alla: AC : CD = GK : FL.

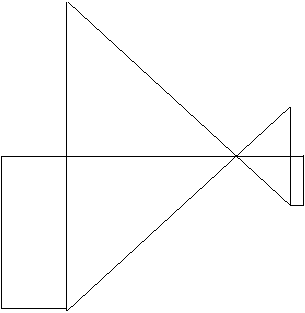A

B

G H C I F

D L

K E

Figura (p. 54 di Ciassi, 1677): si prova che AC : CD = AE : BD dunque,

da GK = HE = AE/2 e FL = ID = BD/2, segue che AC : CD = GK : FL

L’Autore nota che un corpo G posto nella posizione E e sollevato sino al punto A richiede la stessa “forza” (“vis”) richiesta da un corpo F posto in M e sollevato sino a B se e soltanto se i pesi di G e di F sono inversamente proporzionali ai rispettivi bracci GC, FC e quindi alle “altezze” virtualmente percorse AE, BM (come sopra notato, la fisica seicentesca non ha ancora consapevolmente acquisito il concetto di lavoro, e ciò porta all’imprecisione terminologica: la ciassiana “forza” è da interpretarsi in termini di lavoro)[8].

Per apprezzare l’entità delle conclusioni del giovane fisico si noti che affermare che i due pesi P e P’ sono inversamente proporzionali alle altezze virtuali percorse h, h’ equivale ad affermare un’analoga proporzionalità con i quadrati delle velocità v, v’ dei moti di tali pesi (è infatti sufficiente ricordare che l’altezza h è proporzionale al quadrato della velocità di caduta, essendo tale quadrato esprimibile da 2gh). Quindi le considerazioni di Ciassi comportano la proporzionalità diretta della “vis” (e modernamente: dell’energia cinetica) acquisita da un corpo in caduta al quadrato della velocità raggiunta dal corpo.

Come accennato, il risultato ciassiano presentato deve essere storicamente inquadrato nell’ambito della disputa riguardante le forze vive: di notevole rilievo vanno considerate le osservazioni di Ciassi per la soluzione dell’annosa questione, essendo esse in accordo con le decisive affermazioni leibniziane. Inoltre un esame delle date di pubblicazione degli scritti esaminati riserva una sorpresa: la modesta edizione veneziana del Tractatus ciassiano (1677) precede di nove anni la pubblicazione negli Acta Eruditorum Lipsiae (1686) della memoria di Leibniz fondamentale per la risoluzione del problema delle forze vive. Un dettaglio tutt’altro che trascurabile per la storia delle scienze, che potrebbe addirittura rendere proponibili alcune ipotesi: ad esempio, avrebbe senso domandarsi se lo stesso Leibniz fosse a conoscenza, nel 1686, delle considerzioni elaborate, qualche anno prima, dal giovane e sconosciuto Ciassi.

Il confronto di due passi dei due Autori rivela affinità sorprendenti:

- Scrive Ciassi nel 1677: “Un corpo pesante un’oncia, posto con un altro in questo movimento alterno, se sollevato a quattro pollici richiede tanto lavoro quanto un corpo pesante quattro once sollevato ad un pollice”[9].

- Scrive Leibniz nel 1686: “Suppongo che sia necessario altrettanto lavoro per sollevare un corpo del peso di una libbra ad un’altezza di quattro braccia di quanto ne serva per sollevare un corpo di quattro libbre ad un’altezza di un braccio”[10].

Non possiamo non osservare che l’evidente analogia testuale si riferisce soltanto ad una considerazione preliminare, nel contesto della ben più ampia e complessa questione delle forze vive. Inoltre, va sottolineato che anche il principale risultato ciassiano, precedentemente ricordato, non è accompagnato da alcun esplicito riferimento alla grande controversia con gli studiosi della scuola cartesiana, collocazione critica che invece appare chiaramente nella memoria di Leibniz. Non riteniamo quindi sufficiente quanto ora riportato per attribuire direttamente a Ciassi la paternità della soluzione del problema delle forze vive. Possiamo comunque concludere che le ricerche del giovane fisico trevigiano apportano un contributo storicamente apprezzabile al chiarimento di una delle più importanti controversie della meccanica del Seicento.

5. CONCLUSIONI

Quale può (ovvero deve) essere la valenza didattica degli esempi ora presentati? Non riteniamo che la storia della scienza sia sempre direttamente applicabile alla didattica, cioè che l’introduzione agli allievi di una nozione possa comunque seguire l’evoluzione storica di tale concetto: infatti il processo di insegnamento-apprendimento ha luogo oggi, dopo il pieno sviluppo dell’evoluzione storica e può pertanto basarsi anche sui risultati raggiunti nella fase matura di tale sviluppo (Bagni, 2001). Nel caso, ad esempio, del concetto di lavoro, sarebbe almeno discutibile la scelta di far ripercorrere all’allievo la lunga serie di errori e di incertezze concettuali e terminologiche che hanno portato, storicamente, alla faticosa precisazione di tale concetto.

La proposta di alcuni episodi tratti dalla storia della scienza consente però l’introduzione didattica di argomenti importanti ed il chiarimento di dubbi ed incertezze concettuali rilevanti: gli esempi storici e la loro (non sempre facile!) analisi epistemologica possono dunque costituire un preziosissimo, forse addirittura indispensabile patrimonio culturale dell’insegnante, tradursi in una palestra per ragionamenti analogici (seguendo Gian Maria Ciassi, la geometria può essere applicata con successo a chiarire questioni di meccanica!) e costituire quindi un vero e proprio potente strumento didattico[11].

Bibliografia

Bagni, G.T. (1991a), I logaritmi dei numeri negativi in un ‘opuscolo matematico’ (1787) di Francesco Maria Franceschinis, La matematica e la sua didattica, V, 3, 17-22.

Bagni, G.T. (1991b), Gian Maria Ciassi fisico trevigiano, Teorema, Treviso.

Bagni, G.T. (1994), Una «controversia» della matematica del Settecento: i logaritmi dei numeri negativi, Periodico di Matematiche, VII, 2, 2/3, 95-106.

Bagni, G.T. (2000), «Simple» rules and general rules in some High School students’ mistakes, Journal fur Mathematik Didaktik, 21 (2000), 2, 124-138.

Bagni, G.T. (2001), La introducción de la historia de las matemáticas en la enseñanza de los números colmplejos. Una investigación experimental en la educación media superior, Revista Latinoamericana de Investigación en Matemática Educativa, 4, 1, 45-62.

Bagni, G.T. (2002), Mathematical formal models for the learning of Physics: the role of an historical example, Proceedings of GIREP 2001, in via di pubblicazione.

Boncompagni, B. (1840), Biografia del matematico Giuseppe Calandrelli, Giornale Arcadico.

Briggs, H. (1617), Logarithmorum Chilias prima, Londini.

Caldani, P.M. (1782), Della proporzione bernoulliana fra il diametro, e la circonferenza del circolo e dei logaritmi, Lelio Della Volpe, Bologna.

Caldani, P.M. (1791), Riflessioni sopra un opuscolo del P. Franceschinis Barnabita, dei logaritmi dei numeri negativi stampato in Bassano, Soc. Tipografica, Modena.

Calinger, R. (a cura di) (1996), Vita mathematica: historical research and integration with teaching, Mathematical Association of America.

Chevallard, Y. (1985), La transposition didactique, du savoir savant au savoir enseigné, La Penseé Sauvage, Grenoble.

Chuquet, N. (1880), Le Triparty en la Science des Nombres, Marre, A. (a cura di) Bull. bibl. storia math., XIII, 555-659 e 693-814.

Ciassi, G.M. (1677), Meditationes de natura plantarum et Tractatus physicomathematicus De æquilibrio praesertim fluidorum, ac de levitate ignis, Benedetto Miloco, Venezia.

Curtze, M. (1868), Uber die Handschrift ‘Algorismes proportionum magistri Nicolay Orem’, Zeitschr. fur Math. und Phys., XIII, Suppl., 64-79 e 101-104.

D’Amore, B. (1999), Elementi di Didattica della Matematica, Pitagora, Bologna.

De Saint-Vincent, G. (1647), Opus Geometricorum, Antverpiae.

Euler, L. (1749), De la controverse entre Mrs. Leibniz et Bernoulli sur les logarithmes des nombres negatifs et immaginaires, Mem. Acad. des Sciences de Berlin, 5.

Fantuzzi, G. (1778), Notizie della vita e degli scritti di Francesco Maria Zanotti, Stamperia di San Tommaso d’Aquino, Bologna.

Fauvel, J. & van Maanen, J. (1997), Storia e didattica della matematica, Lettera Pristem, 23, 8-13.

Fauvel, J. (1991), For the learning of mathematics (numero speciale sulla storia), 11, 2.

Favaro, A. (1917), I successori di Galileo nello studio di Padova fino alla caduta della Repubblica, N. Archivio Veneto, 65, 1/3.

Ferroni, P. (1782), Magnitudinum exponentialium logarithmorum et trigonometriae sublimis theoria. Nova methodo pertracta, Ex Typographya Allegrimiana, Firenze. Pietro Ferroni fu professore di Matematica all’Università di Pisa; commissario del Granduca di Toscana Pietro Leopoldo, coordinò numerosi lavori di bonifica e riorganizzò la rete stradale.

Fischbein, E. (1987), Intuition in science and mathematics, Reidel, Dodrecht.

Fischbein, E., Nello, M.S. & Marino, M.S. (1991), Factors affecting probabilistic judgments in children and adolescents, Educational Studies in Mathematics, 22, 523-549.

Fontana, G. (1783), Sopra i logaritmi delle quantità negative e sopra gli immaginarj, Mem. della Soc. Ital., I, 183.

Fontana, G. (1799), Sopra la pretesa distinzione fra il nulla reale ed il nulla immaginario, Mem. della Soc. Ital., VIII, 174.

Franceschinis, F.M. (1787), Opuscoli matematici, Remondini, Bassano.

Frisi, P. (1782), Operum tomus primus, algebram et geometriam analyticam continens, Galeazzi, Milano.

Furinghetti, F. & Somaglia, A. (1997), Storia della matematica in classe, L’educazione matematica, XVIII, V, 2, 1.

Furinghetti, F. (1993), Insegnare matematica in una prospettiva storica, L’educazione matematica, III, IV, 123-134.

Giusti, E. (1982), Problemi e metodi di analisi matematica nell’opera di Gianfrancesco Malfatti, Atti del Convegno su Gian Maria Malfatti, Ferrara, 23-24 X 1981, 37-56, Bologna.

Gregory, J. (1677), Vera Circuli et Hyperbolae Quadrature, Patavii.

Grugnetti, L. (1992), L’histoire des mathématiques: une expérience interdisciplinaire fondée sur l’histoire des mathématiques, Plot, 60, 17-21.

Kahneman, D., Slovis, P. & Tversky, A. (1982), Judgement under uncertainity, heuristic and biases, Cambridge University Press, New York.

Langer, R.E. (1935), The life of Leonhard Euler, Scripta mathematica, 3.

Leibniz, G.W. (1768), Opera Omnia, Fratres de Tournes, Genevae.

Leibniz, G.W. (1856), Mathematischen Schriften, Gerhardt, C.I. (a cura di) III, II, Briefwechsel zwiscen Leibniz, Jacob Bernoulli, Johann Bernoulli und Nicolaus Bernoulli, 887, 895, 899, Halle 1856 (ristampa anastatica: Georg Olms Verlagsbuchhandlung 1962).

Loria, G. (1929-1933) Storia delle matematiche dall’alba della civiltà al tramonto del secolo XIX, Sten, Torino 1929-1933 (ristampa: Cisalpino-Goliardica, Milano 1982).

Malfatti, G.F. (1795), Pensieri sulla famosa questione dei logaritmi dei numeri negativi, Mem. Reale Acc. di Sci. Lett. ed Arti di Mantova, 3-54.

Maseres, F. (1791-1807), Scriptores Logaritmici, Londini.

Michieli, A.A. (1944), Una famiglia di matematici e poligrafi trevigiani: i Riccati. II. Vincenzo Riccati, Atti del Reale Istituto Veneto di Scienze, Lettere ed Arti, CIII, II.

Michieli, A.A. (1949a), Le sventure di uno scienziato trevigiano (G.M. Ciassi), Atti dell’Istituto Veneto di Scienze, Lettere ed Arti, CVII, II.

Michieli, A.A. (1949b), Un maestro di Jacopo Riccati (Stefano Degli Angeli), Atti del Reale Istituto Veneto di Scienze, Lettere ed Arti, CVI, II.

Monti, A. (1779), Orazione detta nella Chiesa del S. Salvatore all’occasione de’ solenni funerali del chiar.mo uomo F.M. Zanotti, Stamperia di San Tommaso d’Aquino, Bologna.

Naux, C. (1971), Histoire des logarithmes de Neper a Euler, Blanchard, Paris.

Neper, J. (1619), Mirifici logarithmorum canonis descriptio, Lyon.

Nicolai, G.B. (1754), Lettera da Trevigi, a data 9 novembre 1754, sulla scoperta da lui fatta del libretto del Ciassi, Memorie per servire all’Istoria Letteraria, IV, V.

Nobre, S. (a cura di) (1994), Meeting of the International Study Group on relations between history and pedagogy of mathematics, Blumenau, Brasile 25-27 luglio, UNESP.

Pellizzari, I.A. (1830), Discorso in lode di G.M. Ciassi trivigiano, Giulio Trento, Treviso.

Pepe, L. (1990), Storia e didattica della matematica, L’educazione matematica, III, I-2, 23-33.

Piaget, J. (1980), Experiments in contradictions, Chicago, The University of Chicago Press.

Pizzamiglio, P. (2002), Matematica e storia, La Scuola, Brescia.

Rambaldi, G.B. (1863), Iscrizioni patrie, Longo, Treviso.

Riccati, G. (1778a), Lettera al Signore Iacopo Ab. Pellizzari sopra i logaritmi de’ numeri negativi, Continuazione del Nuovo Giorn. de’ Letterati di Modena, XVI.

Riccati, G. (1778b), Teorema. Il nulla immaginario non può confondersi col nulla reale, Mem. della Soc. Ital., IV, 116.

Riccati, V. (1749), Dialogo, dove ne’ congressi di più giornate delle forze vive e dell’azione delle forze morte si tien discorso, Lelio della Volpe, Bologna.

Riccati, V. (1767), Dieci lettere del P. Vincenzo Riccati all’ab. Jacopo Pellizzari sulla questione della Logistica. Prima raccolta di lettere sopra la questione: Se la Logistica abbia un doppio ramo, Commercio Epist. del Co. Giordano Riccati, XXI, Bibl. Civica di Udine.

Riccati, V. (1789), Sopra i logaritmi dei numeri negativi, Soc. Tipografica, Modena.

Sfard, A. (1991), On the dual nature of mathematical conceptions: reflections on processes and objects as different sides of the same coins, Educational Studies in Mathematics, 22, 1-36.

Stifel, M. (1544), Arithmetica integra, Nuremberg.

Strauss, S. & Bichler, E. (1988), The development of children’s concepts of arithmetic average, Journal for Research in Mathematics Education, 19, 64-80.

Swan, M. (1983), Teaching decimal place value. A comparative study of “conflict” and “positive only” approaches, Shell Centre of Math. Education, Univ. of Nottingham.

Swetz, F.J. (1989), Using problems from the history of mathematics in classroom instruction, Mathematics Teacher, 82, 370-377.

Swetz, F.J. (1995), To know and to teach: mathematical pedagogy from a historical context, Educational Studies in Mathematics, 29, 73-88.

Tall, D. (1990), Inconsistencies in the learning of calculus and analysis, Focus on Learning Problems in Mahematics, 12, 49-64.

Tirosh, D. & Graeber, A. (1990), Inconsistencies in preservice elementary teachers’ beliefs about multiplication and division, Focus on Learning Problems in Mathematics, 12, 65-74.

Tirosh, D. (1990), Inconsistencies in students’ mathematical constructs: Focus on Learning Problems in Mathematics, 12, 111-129.

Tsamir, P. & Tirosh, D. (1997), Metacognizione e coerenza: il caso dell’infinito, La matematica e la sua didattica, 2, 122-131.

Walmesley, C. (1748), Analyse des measures des rapports et des angles, ou reduction des integrations aux logarithmes et aux arcs de cercles, Paris.

Zanotti, F.M. (1752), Della forza de’ corpi che chiamano viva, Eredi di Constantino Pifarri e Giacomo Filippo Primodì, Impressori del S. Officio, Bologna.

---

Back to the main page: è index.htm ç

---

[1] Scrivono J. Fauvel e J. van Maanen: “Come ogni progetto educativo, quello di intendere la storia della matematica come una componente dell’insegnamento della matematica implica un’aspettativa più o meno esplicita in termini di un migliore apprendimento. La ricerca sull’uso della storia della matematica nell’insegnamento è quindi una parte importante della ricerca in didattica della matematica” (Fauvel & van Maanen, 1997, p. 8). F. Furinghetti e A. Somaglia individuano “due livelli di lavoro nell’introduzione della storia nella didattica: uno che potremmo associare a un’immagine ‘sociale’ della matematica e un altro che concerne piuttosto un’immagine ‘interna’ della stessa. Il primo livello si riferisce a quegli interventi mirati a fornire motivazioni allo studio della matematica mediante la contestualizzazione nel sociale [...] Il secondo recupera [...] la dimensione culturale della matematica come metodo” (Furinghetti & Somaglia, 1997, p. 43). Oltre al recente volume di P. Pizzamiglio, moltissime opere sono dedicate alla questione; senza alcuna pretesa di fornire un elenco esauriente, ricordiamo ad esempio: Swetz, 1989 e 1995; Pepe, 1990; Fauvel, 1991; Grugnetti, 1992; Furinghetti, 1993; Nobre, 1994; Calinger, 1996.

[2] Osserviamo sin d’ora che anche la formazione dei docenti è strettamente collegata alle considerazioni esposte: parte delle considerazioni e degli esempi che proporremo nel presente lavoro sono stati trattati nel “Laboratorio di sviluppo curricolare per la storia della matematica” tenuto dall’autore presso la S.S.I.S. del Lazio nel corso dell’a. acc. 2001-2002.

[3] Euler calcolò inoltre i logaritmi dei complessi e dimostrò che essi sono complessi: veniva così provata la chiusura di C rispetto al calcolo del logaritmo e dell’esponenziale.

[4] Per quanto riguarda la riconsiderazione di una risposta data in precedenza, in letteratura troviamo innumerevoli lavori (da: Piaget, 1980). “Molti studi rivelano che spesso gli allievi hanno idee mutuamente incoerenti, occasionalmente come risultato delle loro intuizioni primarie (Fischbein, 1987; Kahnemann, Slovic & Tversky, 1982). Spesso gli studenti ritengono ciascuna di tali incompatibili idee sicura e autoevidente. In molti di questi casi è plausibile che solo uno specifico intervento didattico risolverà le incoerenze (Fischbein, Nello & Marino, 1991) [...] Negli ultimi dieci anni sono stati proposti molti approcci didattici per la risoluzione dell’incoerenza, tra i quali l’insegnamento per conflitto (ad esempio Swan, 1983), l’insegnamento per analogia (ad esempio Strauss & Bichler, 1988) e l’approccio all’ambiente generico (ad esempio Tall, 1990). È stato mostrato che il metodo dell’insegnamento per conflitto, che è basato sull’elevamento della consapevolezza degli studenti delle contraddizioni nelle loro opinioni e della non legittimità di ciò in matematica, può essere efficace per rimuovere [...] molte misconcezioni (Tirosh & Graeber, 1990)” (Tsamir & Tirosh, 1997. Importanti inoltre sono le considerazioni in: Tirosh, 1990; D’Amore, 1999).

[5] Queste sono le considerazioni esposte nello scritto originale leibniziano: “... Suppono, primo corpus cadens ex certa altitudine acquirere vim eousque rursus assurgendi, si directio eius ita ferat, nec quicquam externorum impediat... Suppono item secundo, tanta vi opus esse ad elevandum corpus A unius librae usque ad altitudinem CD quatuor ulnarum, quanta opus est ad elevandum corpus B quatuor librarum, usque ad altitudinem EF unius ulnae... Hinc sequitur corpus A delapsum ex altitudine CD praecise tantum acquisivisse virium, quantum corpus B lapsum ex altitudine EF. Nam corpus A postquam lapsu ex C pervenit ad D, ibi habet vim reassurgendi usque ad C, per suppos. 1, hoc est vim elevandi corpus unius librae (corpus scilicet proprium) ad altitudinem quatuor ulnarum. Et similiter corpus B postquam lapsu ex E pervenit ad F, ibi habet vim reassurgendi usque ad E, per suppos. 1, hoc est vim elevandi corpus quatuor librarum (corpus scilicet proprium) ad altitudinem unius ulnae. Ergo per suppos. 2, vis corporis A existentis in D, et vis corporis B existentis in E, sunt aequales”. E conclude affermando: “Itaque magnum est discrimen inter vim motricem, et quantitatem motus, ita ut unum per alterum aestimari non possit”. Questa importante memoria leibniziana è inclusa nella grande raccolta pubblicata a Ginevra nel 1768 (Leibniz, 1768).

[6] Le posizioni leibniziane sono riflesse anche in: Riccati, 1749 (sul pensiero riccatiano si veda anche Michieli, 1944; Bagni, 1993). In aperto contrasto con Riccati è Zanotti, 1752 (sull’opera di Zanotti indichiamo anche: Fantuzzi, 1778; Monti, 1779).

[7] Il suo Autore nacque a Treviso il 20 marzo 1654 e si formò presso la facoltà di medicina e filosofia dell’Università di Padova, dove ottenne la laurea; i suoi interessi per la matematica lo portarono a frequentare le lezioni di Stefano Degli Angeli nell’ateneo padovano (Favaro, 1917; Michieli, 1949b); secondo alcuni, nello stesso anno della pubblicazione di Meditationes de natura plantarum et Tractatus physicomathematicus, sembra che Ciassi sia stato sul punto di ottenere una cattedra di botanica presso la stessa università (Michieli, 1949a); ma lo studioso si spense prematuramente a Venezia nel 1679.

[8] Proponiamo le interessanti osservazioni ciassiane nel testo originale latino: “Immo haec ipsa altitudinis linearum a motis corporibus descriptarum reciprocatio cum gravitate ipsorum prior causa est, aequalis momenti, quod Galileus non advertit. Etenim corpus cum alio in hac reciprocatione constitutum unam tantum unciam gravitans, ut elevetur ad quatuor pollices, eandem vim requirit, ac corpus gravitans quatuor uncias, ut elevetur ad unum pollicem tantum. Puta ut corpus G unam tantum unciam gravitans attollatur per lineam EA, cuius altitudo sit quatuor pollicum; requiritur eadem vis, ac ut corpus F quatuor uncias gravitans attollatur per lineam DB, cuius altitudo sit tantum unius pollicis. Quia scilicet cum in altitudine lineae EA sint quatuor partes, quarum unaquaeque est aequalis altitudini DB totius; licet ad elevandam corpus G ad singulas harum quatuor partium requireretur alias tantum quarta virium pars, quae requiritur in elevatione corporis F ad equalem altitudinem totius DB; in omnibus tamen simul quatuor partibus EA requiritur quadrupla vis; quia quater ea quarta virium pars replicatur” (Ciassi, 1677, pp. 57-59).

[9] Ciassi, 1677, p. 57; la traduzione è nostra (il termine “lavoro” traduce modernamente la ciassiana “vis”; con il termine “movimento alterno” si indica una leva di primo genere).

[10] Leibniz, 1768, III, pp. 180-181, traduzione nostra (“lavoro” traduce ancora “vis”).

[11] L’autore desidera ringraziare sentitamente la prof. Marisa Michelini dell’Università di Udine per i preziosissimi spunti e suggerimenti.